Sterveelhoek
In de wereld van vandaag is Sterveelhoek een onderwerp geworden dat van groot belang is voor een breed spectrum van mensen. Of het nu professionals zijn die op zoek zijn naar actuele informatie, studenten die hun kennis willen uitbreiden, of gewoon mensen die nieuwsgierig zijn naar meer informatie over dit onderwerp, Sterveelhoek blijft de aandacht trekken van een steeds diverser wordend publiek. In dit artikel zullen we de meest relevante en actuele aspecten met betrekking tot Sterveelhoek grondig onderzoeken, waardoor we een compleet en actueel perspectief op dit onderwerp bieden dat interesse blijft genereren bij alle soorten doelgroepen.

In de meetkunde is een sterveelhoek een complexe veelhoek of combinatie van veelhoeken die op een gestileerde ster lijkt.
Regelmatige sterveelhoeken
Een regelmatige sterveelhoek {n/m} met 1 < m < n / 2 is een figuur met n even lange zijden en n even grote hoeken. Een regelmatige sterveelhoek wordt gevormd door bepaalde diagonalen van een regelmatige n-hoek; steeds wordt een hoekpunt verbonden met de hoekpunten m hoekpunten verderop. Als n en m relatief priem zijn dan is het één zelfdoorsnijdende veelhoek, anders zijn het meerdere al of niet zelfdoorsnijdende veelhoeken door elkaar.
Binnenin ontstaat een kleinere versie van deze regelmatige veelhoek, behalve als de diagonalen door het middelpunt gaan; hoe minder hoekpunten worden overgeslagen hoe groter deze kleinere versie is.
De symmetrie is gelijk aan die van de betreffende regelmatige veelhoek.
 Pentagram |
 Hexagram |
 Heptagram |
 Octagram |
 Enneagram |
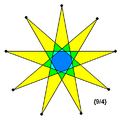 Enneagram |
 Decagram |

| ||||||